Target Trial Emulation in Pregnancy Research

Louisa Smith

2024-10-31

Introduction

pdf

Today’s goals

• Understand the target trial framework and why it’s useful in reproductive and perinatal research
• Explore different types of pregnancy research questions that may be addressed with this approach
• Discover some intuition behind the clone-censor-weighting approach through a numeric example

Why pregnancy research is challenging

• Complex timing issues (exposure, outcomes, competing events)
• Immortal time bias is pervasive
• Multiple individuals (pregnant person, fetus, child)
• Need for clarity about what we’re estimating

One solution

The target trial framework forces us to be explicit about who, what, when, and how (I guess where too, but not usually as much of a problem!)

One problem: time zero

Many observational studies don’t have a clear “time zero” when treatment assignment occurs

Example: Comparing pregnancy outcomes in:

• People who took antidepressants during pregnancy
• People who didn’t take antidepressants during pregnancy

When are they “assigned” to exposure groups?

Immortal time bias

If we define groups based on what actually happened during pregnancy:

• “Exposed” group = those who took medication at some point
• “Unexposed” group = those who never took medication

The exposed group had to survive long enough (e.g. remain pregnant) to take the medication!

• This is a problem whenever the outcome depends on time (i.e., not just survival)

What is a target trial?

A hypothetical randomized trial that would answer your causal question if it could be conducted

Note

The target trial is a design concept, not an analysis method. It has guided study design in epidemiology for decades but recently popularized as an explicit framework (Miguel A. Hernán and Robins 2016).

Why a trial?

Randomized trials have clear advantages for causal inference:

• Randomization at baseline
  • Not the case in observational data no matter what we do, but we can try with good confounder measurement and reasonable eligibility criteria

• Stringent eligibility criteria
  • Everyone who enters the study has equipoise for the treatment strategies being compared

Why a trial?

Randomized trials have clear advantages for causal inference:

• Clear time zero
  • Everyone is assigned to treatment and starts follow-up at the same time
  • We can make this happen in observational data with careful design

• Well-defined treatment strategies
  • In order to give participants their assigned treatment, people have to have rules to follow!
  • We can define these rules in observational data too

Why a target trial?

We know we can’t run the randomized trial we want to conduct to answer our causal question (lack of resources, unethical to randomize, impossible to provide certain treatments/exposures, too many years of follow-up needed, too many treatment strategies to compare, etc.)

• But we can design it hypothetically
• And then try to emulate it as closely as possible with observational data

Emulating a target trial

The observational study should be designed so as to match up with this trial as closely as possible

Warning

Don’t jump straight to emulation without carefully thinking through the trial, though it can be helpful to think ahead. Compromises in emulation should be explicit and justified.

Essential components

1. Eligibility criteria
2. Treatment strategies
3. Assignment procedures
4. Follow-up period
5. Outcome(s)
6. Causal contrast(s)
7. Statistical analysis plan

Note

Recently published guidelines for reporting target trial emulations detail these components: Cashin et al. (2025)

Eligibility criteria: the “who”

Besides making for a clearer question with more practical implications, eligibility criteria can help address confounding in the emulation by ensuring everyone included has a reasonable chance of getting the treatment strategies being compared*

• We might exclude people with contraindications to treatment, or those who would never consider it
• This often means defining pregnancy status and gestational age at time zero carefully

*Always need positivity: everyone included must have some non-zero probability of receiving each treatment strategy being compared

Time zero: the “when”

The eligibility criteria also define when people enter the study

• Time zero occurs when people meet eligibility criteria (and in a trial, agree to be randomized)
• We could imagine scenarios where people meet eligibility repeatedly over time (e.g., at every antenatal care visit)
  • We can take this into account when emulating

Treatment strategies: the “what” and “how”

Each strategy represents an intervention we could imagine putting in motion at time zero for a given treatment arm:

• Immediately upon randomization, tell everyone to get treatment (e.g., a vaccination)
• At 6 weeks gestation (time zero), tell everyone to start treatment at 12 weeks gestation but not before
• Tell everyone to wait until 20 weeks to start treatment
• Tell everyone to start treatment when symptoms appear

This is easier for some causal questions than others

• Pharmaceutical interventions with fixed timing (e.g., vaccination at week 32 vs. no vaccination)
• Procedure at some known clinical event (e.g., cerclage at diagnosis of short cervix vs. no cerclage)
• Comparisons of two treatments with the same indication

Tip

It’s helpful to read through existing randomized trials on similar questions to see how they defined these components, see clinicaltrials.gov for ideas!

Pharmaceutical example (Zidan et al. (2025))

Components	Target trial
Causal question	What is the effect of SARS-CoV-2 mRNA vaccine BNT162b2 on COVID-19?
Eligibility criteria	Inclusion criteria: Healthy women ≥18 years of age who are between 24 0/7 and 34 0/7 weeks’ gestation on the day of planned vaccination, with an uncomplicated, singleton pregnancy. Healthy participants determined by medical history, physical examination, and clinical judgment to be appropriate for inclusion in the study. Documented negative HIV antibody test. Exclusion criteria: Other medical or psychiatric condition including recent (within the past year) or active suicidal ideation/behavior. Previous clinical or microbiological diagnosis of COVID-19. Participants with known or suspected immunodeficiency. Bleeding diathesis or condition associated with prolonged bleeding. Previous vaccination with any COVID-19 vaccine. Current alcohol abuse or illicit drug use. Participants who receive treatment with immunosuppressive therapy.
Treatment strategies	1. Two vaccination doses 2. No SARS-CoV-2 vaccination until the end of pregnancy
Assignment procedures	1:1 randomization into the two treatment arms, stratified by gestational week
Follow-up	Since administering the first dose and up to 1 month post delivery
Outcome	SARS-CoV-2 infection as determined by positive PCR test or clinical COVID-19 diagnosis
Causal contrast	Incidence rate ratios; intention-to-treat (one vaccine dose) and per-protocol (two doses)

Other types of questions

It may feel weird to design a target trial for other types of causal questions

• Unethical/impossible to randomize
  • e.g., harmful exposures, social determinants of health

It’s worth thinking through anyway to make sure you are clear about your causal question of interest (you don’t have to publish it as a “target trial”!)

Non-pharmaceutical example (Smith et al. (2022))

Components	Target trial
Causal question	What is the effect of COVID-19 infection on preterm delivery?
Eligibility criteria	1. Pregnant individuals with gestational age 12-36 weeks. 2. No known previous SARS-CoV-2 infection 3. No previous vaccination for COVID-19
Treatment strategies	1. Symptomatic COVID-19 within a week after enrollment. 2. No SARS-CoV-2 infection for the rest of the pregnancy.
Assignment procedures	Randomization at enrollment, stratified by gestational age (in weeks).
Follow-up	Patients are followed from the time of COVID-19 testing or enrollment (time zero) until delivery, loss to follow-up, or administrative end of follow-up.
Outcome	Preterm delivery, defined as delivery before 37 completed weeks of gestation.
Causal contrast	Intention-to-treat effect on the risk ratio and risk difference scales for each gestational week (time zero)

Notes on these components and things to think about in emulation (hopefully not compromises to the integrity of the target trial)

Components	Target trial
Eligibility criteria	Based only on pre-baseline characteristics Generally requires pre-baseline observation window
Treatment strategies	Won’t be able to emulate actual placebo or blinding (can assign no treatment if realistic) Some people must have “adhered” to the treatment strategy
Assignment procedures	Randomization (within levels of confounders) is always an assumption Assignment “happens” as soon as someone meets eligibility criteria
Follow-up	Monitoring for the outcome throughout follow-up (e.g., SARS-CoV-2 testing) may need to be part of the treatment strategy
Outcome	Outcome ascertainment can’t be blinded in emulation
Causal contrast	Intention-to-treat effect makes sense when “most” of the treatment happens immediately upon randomization Per-protocol useful when you don’t know right away who starts what treatment

Examples

Avalos et al. (2023)

Caniglia et al. (2018)

Chiu et al. (2024)

Wong et al. (2024)

Discussion

1. What was the causal question?
2. What were the key components of the target trial protocol, including eligibility criteria, treatment strategies, etc. What was time zero?
3. What made this question challenging to design an “emulatable” target trial?
4. How did the authors handle the challenge? Were there compromises made?

Avalos et al. (2023) - Treating hypertension at different thresholds

Key features/challenges:

• Treatment strategies are dynamic - depend on clinical measurements, don’t know ahead of time who will need treatment when
• People can be part of multiple treatment groups over time

Caniglia et al. (2018) - Antiretroviral therapy started before conception

Key features/challenges:

• Treatment/time zero occurs before pregnancy
• Competing event: not getting pregnant
• Can’t condition on pregnancy without bias
• Treatment strategy includes getting pregnant within a certain time frame

Chiu et al. (2024) - Metformin in first trimester

Key features/challenges:

• Treatment happens early in pregnancy
• Competing risks: pregnancy loss – can’t observe malformations without live birth
• Use of composite outcome

Wong et al. (2024) - COVID-19 antiviral within 5 days of infection

Key features/challenges:

• Treatment must start within a short window after infection (grace period)
• Rare exposure, rare outcomes

Common themes across papers

1. Time zero must be clearly defined
   • Before hypertension (Avalos)
   • Preconception (Caniglia)
   • Early pregnancy (Chiu)
   • At sympomatic infection (Wong)

2. Strategies must be realistic and well-defined
   • Not just “exposed vs. unexposed”
   • Include rules for what happens over time, e.g., grace period, blood pressure monitoring

3. Competing events are common in pregnancy
   • Not conceiving competes with pregnancy outcomes
   • Pregnancy loss competes with later outcomes

Thoughts/questions

Emulating target trials with clone-censor weighting

This example is somewhat based on an example about comparing duration of treatment in Miguel A. Hernán (2018)

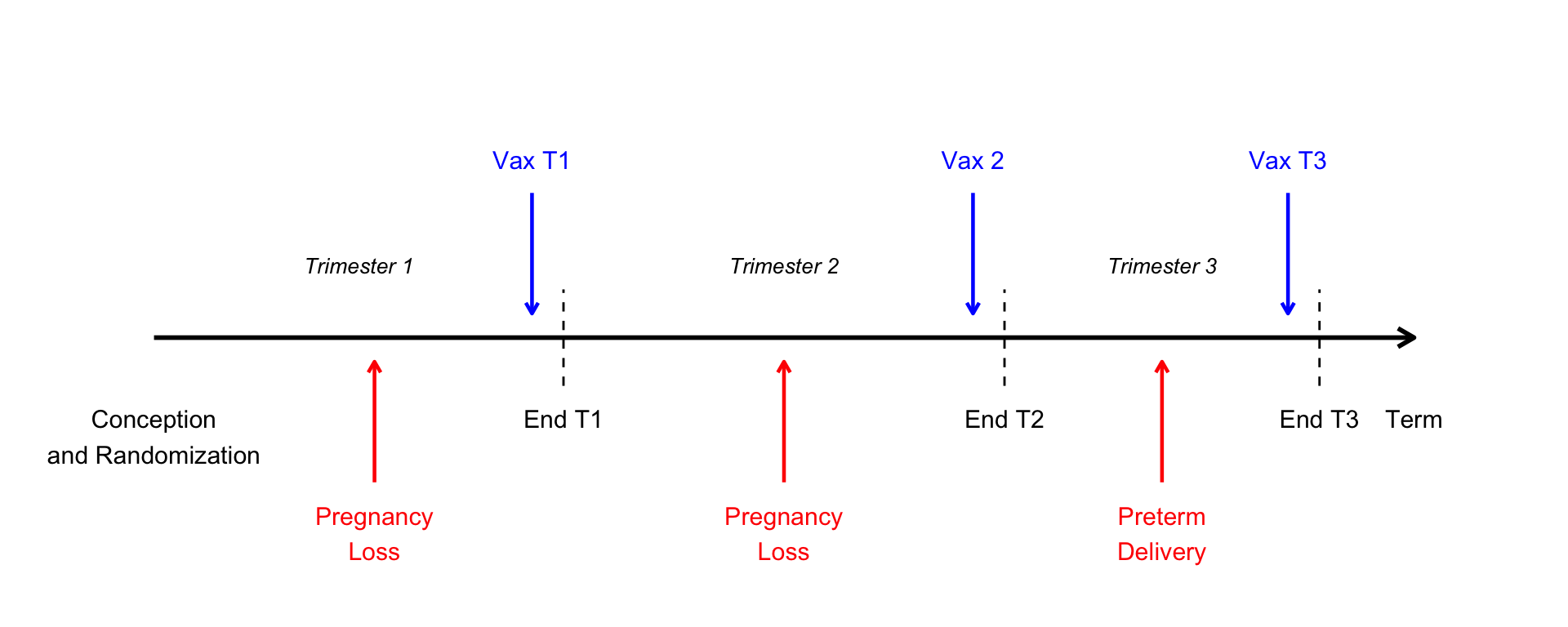
Does vaccination timing in pregnancy affect live birth?

Eligibility: Unvaccinated, at/soon after conception

Treatment strategies:

• Strategy 0: Never vaccinate during pregnancy
• Strategy 1: Vaccinate in trimester 1 only
• Strategy 2: Vaccinate in trimester 2 only
• Strategy 3: Vaccinate in trimester 3 only

Outcome: Live birth (yes/no)

Pregnancy timeline

Note

We are simplifying things by assuming vaccination happens at the end of a trimester, after any pregnancy losses

Randomized trial data

16 pregnant people randomly assigned to 4 strategies:

Person	Assigned strategy	Loss T1	Vax T1	Loss T2	Vax T2	Preterm	Vax T3	Term birth	Live birth
A	0	0	0	0	0	0	0	1	1
B	0	0	0	0	0	1	-	-	1
C	0	0	0	1	-	-	-	-	0
D	0	1	-	-	-	-	-	-	0
E	1	0	1	0	0	0	0	1	1
F	1	0	1	0	0	1	-	-	1
G	1	0	1	1	-	-	-	-	0
H	1	1	-	-	-	-	-	-	0
I	2	0	0	0	1	0	0	1	1
J	2	0	0	0	1	1	-	-	1
K	2	0	0	1	-	-	-	-	0
L	2	1	-	-	-	-	-	-	0
M	3	0	0	0	0	0	1	1	1
N	3	0	0	0	0	1	-	-	1
O	3	0	0	1	-	-	-	-	0
P	3	1	-	-	-	-	-	-	0

Randomized trial results

By assigned strategy:

Assigned strategy	N	Live births	Probability
0	4	2	0.5
1	4	2	0.5
2	4	2	0.5
3	4	2	0.5

All strategies have 50% live birth rate (we are operating in a situation where the null hypothesis of no effect of vaccination at any time is true)

Moving to observational data

In observational data, we don’t see the assigned strategy.

We only see what actually happened:

• When (if) people got vaccinated
• When pregnancy losses occurred
• Whether there was a live birth and when

Let’s classify people by observed vaccination status and timing…

Observed data

Same 16 people, but now we don’t know their assigned strategy:

Person	Observed treatment	Loss T1	Vax T1	Loss T2	Vax T2	Preterm	Vax T3	Term birth	Live birth
A	0 (Never)	0	0	0	0	0	0	1	1
B	0 (Never)	0	0	0	0	1	-	-	1
C	0 (Never)	0	0	1	-	-	-	-	0
D	0 (Never)	1	-	-	-	-	-	-	0
E	1 (Vax T1)	0	1	0	0	0	0	1	1
F	1 (Vax T1)	0	1	0	0	1	-	-	1
G	1 (Vax T1)	0	1	1	-	-	-	-	0
H	0 (Never)	1	-	-	-	-	-	-	0
I	2 (Vax T2)	0	0	0	1	0	0	1	1
J	2 (Vax T2)	0	0	0	1	1	-	-	1
K	0 (Never)	0	0	1	-	-	-	-	0
L	0 (Never)	1	-	-	-	-	-	-	0
M	3 (Vax T3)	0	0	0	0	0	1	1	1
N	0 (Never)	0	0	0	0	1	-	-	1
O	0 (Never)	0	0	1	-	-	-	-	0
P	0 (Never)	1	-	-	-	-	-	-	0

Naive analysis: by achieved vaccination

Classify by when they actually got vaccinated:

Observed vaccination	N	Live births	Probability
0 (Never)	10	3	0.30
1 (Vax T1)	3	2	0.67
2 (Vax T2)	2	2	1.00
3 (Vax T3)	1	1	1.00

The problem: immortal time bias!

Later vaccination appears highly protective!

But: People who got vaccinated later had to survive to that point

• All of the pregnancy losses get assigned to the “Never” or “Vax T1” groups
• By the time people are classified as “Vax T2” or “Vax T3”, they have already survived those earlier periods

Think like a randomized trial

In a randomized trial, people are assigned to strategies at time zero – even if they don’t get treatment (by choice, not surviving long enough, etc.), they are analyzed in their assigned group*

*In an intention-to-treat analysis. Even under randomized assignment, an “as-treated” analysis would have the same problem if people are classified by what they actually did

Immortal time bias

Generally the not-treated group will underestimate the true risk, and the treated group will overestimate it (the later treated, or longer duration required, the more the bias):

Strategy	True probability	Naive estimate	Bias
0 (Never)	0.50	0.30	↓
1 (Vax T1)	0.50	0.67	↑
2 (Vax T2)	0.50	1.00	↑↑
3 (Vax T3)	0.50	1.00	↑↑

This makes treatment appear to reduce risk when there is actually no effect (or if there were a true effect of treatment, this might mask it)

Emulation via clone-censor-weighting

Pretend you have a randomized trial in which everyone is assigned to all strategies at time zero:

1. Clone everyone to all compatible strategies
2. Censor clones when they deviate from assigned strategy
3. Weight to correct for selection bias from censoring

Step 1: Cloning

For each person, create clones for all treatment strategies

Person	Assigned strategy	Loss T1	Vax T1	Loss T2	Vax T2	Preterm	Vax T3	Term birth	Live birth
A-0	0	0	0	0	0	0	0	1	1
B-0	0	0	0	0	0	1	-	-	1
C-0	0	0	0	1	-	-	-	-	0
D-0	0	1	-	-	-	-	-	-	0
E-0	0	0	1	0	0	0	0	1	1
F-0	0	0	1	0	0	1	-	-	1
G-0	0	0	1	1	-	-	-	-	0
H-0	0	1	-	-	-	-	-	-	0
I-0	0	0	0	0	1	0	0	1	1
J-0	0	0	0	0	1	1	-	-	1
K-0	0	0	0	1	-	-	-	-	0
L-0	0	1	-	-	-	-	-	-	0
M-0	0	0	0	0	0	0	1	1	1
N-0	0	0	0	0	0	1	-	-	1
O-0	0	0	0	1	-	-	-	-	0
P-0	0	1	-	-	-	-	-	-	0

Treatment strategy Vax T1

Person	Assigned strategy	Loss T1	Vax T1	Loss T2	Vax T2	Preterm	Vax T3	Term birth	Live birth
A-1	1	0	0	0	0	0	0	1	1
B-1	1	0	0	0	0	1	-	-	1
C-1	1	0	0	1	-	-	-	-	0
D-1	1	1	-	-	-	-	-	-	0
E-1	1	0	1	0	0	0	0	1	1
F-1	1	0	1	0	0	1	-	-	1
G-1	1	0	1	1	-	-	-	-	0
H-1	1	1	-	-	-	-	-	-	0
I-1	1	0	0	0	1	0	0	1	1
J-1	1	0	0	0	1	1	-	-	1
K-1	1	0	0	1	-	-	-	-	0
L-1	1	1	-	-	-	-	-	-	0
M-1	1	0	0	0	0	0	1	1	1
N-1	1	0	0	0	0	1	-	-	1
O-1	1	0	0	1	-	-	-	-	0
P-1	1	1	-	-	-	-	-	-	0

And so on…

Step 2: Censoring

Censor clones when their observed data becomes incompatible with assigned strategy:

• Strategy 0 (never): censor if vaccinated in T1, T2, or T3
• Strategy 1 (vax T1): censor if not vaccinated in T1
• Strategy 2 (vax T2): censor if vaccinated in T1 or not vaccinated in T2
• Strategy 3 (vax T3): censor if vaccinated in T1 or T2 or not vaccinated in T3

If there is a pregnancy loss in T1, do not censor afterward–we don’t know whether they would have gotten vaccinated or not (can contribute to multiple strategies)

Censoring

• This is why defining the treatment strategies precisely is incredibly important, more so than in a real trial
  • In real life, “clinical judgment” may result in someone stopping treatment
  • In your emulation, should you censor someone if they stop treatment? Or would they be “allowed” to stop in a real trial?
• If everyone ends up censored, you’re trying to study a treatment strategy for which you have no positivity!
  • Come up with a new strategy that allows more flexibility!

Practice censoring

Picture

Data

Step 3: Weighting

Selection bias introduced by censoring must be corrected

Use inverse probability weighting:

• Weight = 1 / (probability of remaining uncensored)
  • This would be conditional on current values of covariates if we had them
• Transfers weight from censored to uncensored observations

Calculating probability of remaining uncensored

This varies over time, and can be calculated as the product of interval-specific probabilities:

\[ \text{Prob(uncensored at time } t) = \prod_{k=0}^{t} \text{Prob(uncensored at } k \mid \text{uncensored at } k-1) \]

That is, the probability of still being uncensored at the end of T3 is:

the probability of not being censored in T1

times the probability of not being censored in T2 (given not censored in T1)

times the probability of not being censored in T3 (given not censored in T1 or T2)

Original Data

library(tidyverse)

trial_data <- read_csv("ccw-example-data.csv")
trial_data

# A tibble: 16 × 10
   person assigned loss_t1 vax_t1 loss_t2 vax_t2 preterm vax_t3  term livebirth
   <chr>     <dbl>   <dbl>  <dbl>   <dbl>  <dbl>   <dbl>  <dbl> <dbl>     <dbl>
 1 A             0       0      0       0      0       0      0     1         1
 2 B             0       0      0       0      0       1     NA    NA         1
 3 C             0       0      0       1     NA      NA     NA    NA         0
 4 D             0       1     NA      NA     NA      NA     NA    NA         0
 5 E             1       0      1       0      0       0      0     1         1
 6 F             1       0      1       0      0       1     NA    NA         1
 7 G             1       0      1       1     NA      NA     NA    NA         0
 8 H             1       1     NA      NA     NA      NA     NA    NA         0
 9 I             2       0      0       0      1       0      0     1         1
10 J             2       0      0       0      1       1     NA    NA         1
11 K             2       0      0       1     NA      NA     NA    NA         0
12 L             2       1     NA      NA     NA      NA     NA    NA         0
13 M             3       0      0       0      0       0      1     1         1
14 N             3       0      0       0      0       1     NA    NA         1
15 O             3       0      0       1     NA      NA     NA    NA         0
16 P             3       1     NA      NA     NA      NA     NA    NA         0

Step 1: Cloning

Each person is cloned into 4 copies (one for each vaccination strategy: 0, 1, 2, 3)

cloned_data <- trial_data %>%
  crossing(strategy = 0:3) %>%
  relocate(strategy, .after = person)

cloned_data %>%
  count(strategy)

# A tibble: 4 × 2
  strategy     n
     <int> <int>
1        0    16
2        1    16
3        2    16
4        3    16

16 people × 4 strategies = 64 rows

Step 2: Censoring

censored_data <- cloned_data %>%
  mutate(
    # T1: only at risk if survived T1
    censored_t1 = case_when(
      loss_t1 == 1 ~ NA,  # Already had outcome
      strategy %in% c(0, 2, 3) & vax_t1 == 1 ~ TRUE,  # Deviated by vaccinating
      strategy == 1 & vax_t1 == 0 ~ TRUE,  # Deviated by not vaccinating
      .default = FALSE  # Followed strategy
    ),
    
    # T2: only at risk if uncensored and unvaccinated at T1 and survived T2
    censored_t2 = case_when(
      is.na(censored_t1) | censored_t1 ~ NA,  # Already censored or had outcome at T1
      loss_t2 == 1 ~ NA,  # Had outcome at T2
      vax_t1 == 1 ~ NA,  # Already had vax at T1
      strategy %in% c(0, 3) & vax_t2 == 1 ~ TRUE,  # Deviated by vaccinating
      strategy == 2 & vax_t2 == 0 ~ TRUE,  # Deviated by not vaccinating
      .default = FALSE  # Followed strategy
    ),
    
    # T3: only at risk if uncensored and unvaccinated at T2 and survived T3
    censored_t3 = case_when(
      is.na(censored_t2) | censored_t2 ~ NA,  # Already censored or had outcome at T2
      preterm == 1 ~ NA,  # Had outcome at T3
      vax_t1 == 1 | vax_t2 == 1 ~ NA,  # Already had vax at T1 or T2
      strategy == 0 & vax_t3 == 1 ~ TRUE,  # Deviated by vaccinating
      strategy == 3 & vax_t3 == 0 ~ TRUE,  # Deviated by not vaccinating
      .default = FALSE  # Followed strategy
    ),
    
    # Final censoring: censored if ANY time point is TRUE
    censored = (censored_t1) | (censored_t2) | (censored_t3),
    censored = replace_na(censored, FALSE)
  )

Censoring Summary

Different numbers contribute to each strategy:

censored_data %>%
  group_by(strategy) %>%
  summarise(
    n_total = n(),
    censored_t1 = sum(censored_t1 == TRUE, na.rm = TRUE),
    censored_t2 = sum(censored_t2 == TRUE, na.rm = TRUE),
    censored_t3 = sum(censored_t3 == TRUE, na.rm = TRUE),
    total_censored = sum(censored),
    uncensored = sum(!censored)
  )

# A tibble: 4 × 7
  strategy n_total censored_t1 censored_t2 censored_t3 total_censored uncensored
     <int>   <int>       <int>       <int>       <int>          <int>      <int>
1        0      16           3           2           1              6         10
2        1      16           9           0           0              9          7
3        2      16           3           4           0              7          9
4        3      16           3           2           1              6         10

Step 3a: Calculate Censoring Probabilities

Probability of vaccination can be used to calculate interval-specific censoring probabilities

1. Set up the data so that people who aren’t eligible to be censored at a given timepoint don’t contribute (have NA for vaccination status and/or subset to those not previously censored or vaccinated
2. Model the probability of treatment (i.e., a propensity score model!)

Vaccination in T1 = censoring (strategy 0, 2, and 3) or not (strategy 1)

trial_data |>
  filter(!is.na(vax_t1)) |>
  pull(vax_t1, name = person)

A B C E F G I J K M N O 
0 0 0 1 1 1 0 0 0 0 0 0 

mod_vax_t1 <- glm(vax_t1 ~ 1, data = trial_data, family = binomial())
p_vax_t1 <- predict(mod_vax_t1, type = "response")[1] # all have same predicted value because no covariates
p_vax_t1

   1 
0.25 

Vaccination in T2 = censoring (strategy 0 and 3) or not (2)

(For strategy 1, already censored if not vaccinated in T1 so no one “at risk for” censoring here)

trial_data |>
  filter(vax_t1 == 0, !is.na(vax_t2)) |>
  pull(vax_t2, name = person)

A B I J M N 
0 0 1 1 0 0 

mod_vax_t2 <- glm(vax_t2 ~ 1, data = trial_data, family = binomial(),
                  subset = vax_t1 == 0)
p_vax_t2 <- predict(mod_vax_t2, type = "response")[1]
p_vax_t2

        1 
0.3333333 

Vaccination in T3 = censoring (strategy 0) or not (3)

(For strategies 1 and 2, already censored if not vaccinated in T1 or T2 so no one “at risk for” censoring here)

trial_data |>
  filter(vax_t1 == 0, vax_t2 == 0, !is.na(vax_t3)) |>
  pull(vax_t3, name = person)

A M 
0 1 

mod_vax_t3 <- glm(vax_t3 ~ 1, data = trial_data, family = binomial(), subset = vax_t1 == 0 & vax_t2 == 0)
p_vax_t3 <- predict(mod_vax_t3, type = "response")[1]
p_vax_t3

  1 
0.5 

Step 3b: Calculate Weights

Weight = 1 / (cumulative probability of not being censored)

weighted_data <- censored_data %>%
  mutate(
    # Probability of not being censored at each time point
    prob_not_cens_t1 = case_when(
      is.na(censored_t1) ~ 1,  # Not at risk
      strategy == 1 ~ p_vax_t1,  # Strategy 1: needs vax at T1
      strategy %in% c(0, 2, 3) ~ 1 - p_vax_t1,  # No vax at T1
      TRUE ~ 1
    ),
    
    prob_not_cens_t2 = case_when(
      is.na(censored_t2) ~ 1,  # Not at risk
      strategy == 2 ~ p_vax_t2,  # Strategy 2: needs vax at T2
      strategy %in% c(0, 3) ~ 1 - p_vax_t2,  # No vax at T2
      TRUE ~ 1
    ),
    
    prob_not_cens_t3 = case_when(
      is.na(censored_t3) ~ 1,  # Not at risk
      strategy == 3 ~ p_vax_t3,  # Strategy 3: needs vax at T3
      strategy == 0 ~ 1 - p_vax_t3,  # No vax at T3
      TRUE ~ 1
    ),
    
    # Cumulative probability = product
    cum_prob_not_censored = prob_not_cens_t1 * prob_not_cens_t2 * prob_not_cens_t3,
    
    # Weight = inverse probability (only for uncensored)
    weight = if_else(!censored, 1 / cum_prob_not_censored, 0)
  )

Example: Strategy 0 (Never vaccinate)

Uncensored individuals and their weights:

weighted_data %>%
  filter(strategy == 0, !censored) %>%
  select(person, livebirth, weight)

# A tibble: 10 × 3
   person livebirth weight
   <chr>      <dbl>  <dbl>
 1 A              1   4.00
 2 B              1   2.00
 3 C              0   1.33
 4 D              0   1   
 5 H              0   1   
 6 K              0   1.33
 7 L              0   1   
 8 N              1   2.00
 9 O              0   1.33
10 P              0   1   

Step 3c: Calculate Weighted Outcomes

weighted_data %>%
  filter(!censored) %>%
  group_by(strategy) %>%
  summarise(
    sum_weights = sum(weight),
    weighted_livebirths = sum(livebirth * weight),
    risk_livebirth = weighted_livebirths / sum_weights
  )

# A tibble: 4 × 4
  strategy sum_weights weighted_livebirths risk_livebirth
     <int>       <dbl>               <dbl>          <dbl>
1        0        16.0                8.00          0.500
2        1        16.0                8.00          0.500
3        2        16.0                8.00          0.500
4        3        16.0                8.00          0.500

Why it works

The three steps:

1. Cloning eliminates immortal time bias by assigning strategies at time zero
2. Censoring ensures clones follow their assigned strategy
3. Weighting corrects for selection bias introduced by censoring

Key assumptions

• No unmeasured confounding (of baseline treatment and treatment continuation/discontinuation, i.e., time-varying confounding)
• Correct specification of censoring models
  • There are many different modeling assumptions we could make, e.g., one model for vaccination with a term for time, or separate models at each time point
• Positivity (some probability of continuing the treatment strategy at each time)

When to use clone-censor-weighting

• Treatment duration comparisons
• Sustained treatment strategies that evolve over time
• Variable timing of exposure
• Threshold-based or dynamic treatment rules
• Any strategy where assignment isn’t identifiable at time zero
• Multiple cycles or sequential treatment decisions

Practical considerations

• Descriptive analysis of treatment patterns
• Check positivity (can strategies actually be followed?)
• How will you define confounders (both baseline and time-varying)
• Start with simple examples to develop code
• Check weight distributions

Extensions and advanced topics

• Grace periods for treatment initiation
• Nested sequential trials
• Joint strategies (treatment + monitoring)

Helpful/interesting papers

Miguel A. Hernán et al. (2008) Cain et al. (2010) Young et al. (2011) Miguel A. Hernán et al. (2016) Miguel A. Hernán and Robins (2016) Labrecque and Swanson (2017) Miguel A. Hernán (2018) Caniglia et al. (2019) Dickerman et al. (2019) Chiu et al. (2020) Maringe et al. (2020) Ben-Michael, Feller, and Stuart (2021) Gaber et al. (2024) Cashin et al. (2025) (fu2025starting?) Moreno-Betancur, Wijesuriya, and Carlin (2025)

Discussion/Questions

1. What pregnancy research questions are you working on?

2. How might you apply target trial thinking?

3. What challenges do you anticipate?

4. What tools or resources would be most helpful?

Thank you!

email: l.smith@northeastern.edu

References

Avalos, Lyndsay A., Romain S. Neugebauer, Nerissa Nance, Sylvia E. Badon, T. Craig Cheetham, Thomas R. Easterling, Kristi Reynolds, et al. 2023. “Maternal and Neonatal Outcomes Associated with Treating Hypertension in Pregnancy at Different Thresholds.” Pharmacotherapy: The Journal of Human Pharmacology and Drug Therapy 43 (5): 381–90. https://doi.org/10.1002/phar.2778.

Ben-Michael, Eli, Avi Feller, and Elizabeth A. Stuart. 2021. “A Trial Emulation Approach for Policy Evaluations with Group-Level Longitudinal Data.” Epidemiology 32 (4): 533–40. https://doi.org/10.1097/ede.0000000000001369.

Cain, Lauren E., James M. Robins, Emilie Lanoy, Roger Logan, Dominique Costagliola, and Miguel A. Hernán. 2010. “When to Start Treatment? A Systematic Approach to the Comparison of Dynamic Regimes Using Observational Data.” The International Journal of Biostatistics 6 (2): 1–42. https://doi.org/10.2202/1557-4679.1212.

Caniglia, Ellen C., James M. Robins, Lauren E. Cain, Caroline Sabin, Roger Logan, Sophie Abgrall, Michael J. Mugavero, et al. 2019. “Emulating a Trial of Joint Dynamic Strategies: An Application to Monitoring and Treatment of HIV-positive Individuals.” Statistics in Medicine 38 (13): 2428–46. https://doi.org/10.1002/sim.8120.

Caniglia, Ellen C., Rebecca Zash, Denise L. Jacobson, Modiegi Diseko, Gloria Mayondi, Shahin Lockman, Jennifer Y. Chen, et al. 2018. “Emulating a Target Trial of Antiretroviral Therapy Regimens Started Before Conception and Risk of Adverse Birth Outcomes.” AIDS 32 (1): 113–20. https://doi.org/10.1097/qad.0000000000001673.

Cashin, Aidan G., Harrison J. Hansford, Miguel A. Hernán, Sonja A. Swanson, Hopin Lee, Matthew D. Jones, Issa J. Dahabreh, et al. 2025. “Transparent Reporting of Observational Studies Emulating a Target Trial: The TARGET Statement.” BMJ 390 (September): e087179. https://doi.org/10.1136/bmj-2025-087179.

Chiu, Yu-Han, Krista F. Huybrechts, Elisabetta Patorno, Jennifer J. Yland, Carolyn E. Cesta, Brian T. Bateman, Ellen W. Seely, Miguel A. Hernán, and Sonia Hernández-Díaz. 2024. “Metformin Use in the First Trimester of Pregnancy and Risk for Nonlive Birth and Congenital Malformations: Emulating a Target Trial Using Real-World Data.” Annals of Internal Medicine 177 (7): 862–70. https://doi.org/10.7326/M23-2038.

Chiu, Yu-Han, Mats J. Stensrud, Issa J. Dahabreh, Paolo Rinaudo, Michael P. Diamond, John Hsu, Sonia Hernández-Díaz, and Miguel A. Hernán. 2020. “The Effect of Prenatal Treatments on Offspring Events in the Presence of Competing Events: An Application to a Randomized Trial of Fertility Therapies.” Epidemiology 31 (5): 636. https://doi.org/10.1097/EDE.0000000000001222.

Dickerman, Barbra A., Xabier García-Albéniz, Roger Logan, Spiros Denaxas, and Miguel A. Hernán. 2019. “Avoidable Flaws in Observational Analyses: An Application to Statins and Cancer.” Nature Medicine 25 (10): 1601–6. https://doi.org/10.1038/s41591-019-0597-x.

Gaber, Charles E., Kent A. Hanson, Sodam Kim, Jennifer L. Lund, Todd A. Lee, and Eleanor J. Murray. 2024. “The Clone-Censor-Weight Method in Pharmacoepidemiologic Research: Foundations and Methodological Implementation.” Current Epidemiology Reports, February. https://doi.org/10.1007/s40471-024-00346-2.

Hernán, Miguel A. 2018. “How to Estimate the Effect of Treatment Duration on Survival Outcomes Using Observational Data.” BMJ 360 (February): k182. https://doi.org/10.1136/bmj.k182.

Hernán, Miguel A., Alvaro Alonso, Roger Logan, Francine Grodstein, Karin B. Michels, Walter C. Willett, Joann E. Manson, and James M. Robins. 2008. “Observational Studies Analyzed Like Randomized Experiments: An Application to Postmenopausal Hormone Therapy and Coronary Heart Disease.” Epidemiology 19 (6): 766–79. https://doi.org/10.1097/ede.0b013e3181875e61.

Hernán, Miguel A., and James M. Robins. 2016. “Using Big Data to Emulate a Target Trial When a Randomized Trial Is Not Available.” American Journal of Epidemiology 183 (8): 758–64. https://doi.org/10.1093/aje/kwv254.

Hernán, Miguel A., Brian C. Sauer, Sonia Hernández-Díaz, Robert Platt, and Ian Shrier. 2016. “Specifying a Target Trial Prevents Immortal Time Bias and Other Self-Inflicted Injuries in Observational Analyses.” Journal of Clinical Epidemiology 79: 70–75. https://doi.org/10.1016/j.jclinepi.2016.04.014.

Labrecque, Jeremy A., and Sonja A. Swanson. 2017. “Target Trial Emulation: Teaching Epidemiology and Beyond.” European Journal of Epidemiology 32 (6): 473–75. https://doi.org/10.1007/s10654-017-0293-4.

Maringe, Camille, Sara Benitez Majano, Aimilia Exarchakou, Matthew Smith, Bernard Rachet, Aurélien Belot, and Clémence Leyrat. 2020. “Reflection on Modern Methods: Trial Emulation in the Presence of Immortal-Time Bias. Assessing the Benefit of Major Surgery for Elderly Lung Cancer Patients Using Observational Data.” International Journal of Epidemiology 49 (5): 1719–29. https://doi.org/10.1093/ije/dyaa057.

Moreno-Betancur, Margarita, Rushani Wijesuriya, and John B. Carlin. 2025. “The Ideal Trial: Defining Causal Estimands That Balance Relevance and Feasibility in Target Trial Emulations and Actual Randomized Trials.” arXiv. https://doi.org/10.48550/arXiv.2405.10026.

Smith, Louisa H., Camille Y. Dollinger, Tyler J. VanderWeele, Diego F. Wyszynski, and Sonia Hernández-Díaz. 2022. “Timing and Severity of COVID-19 During Pregnancy and Risk of Preterm Birth in the International Registry of Coronavirus Exposure in Pregnancy.” BMC Pregnancy and Childbirth 22 (1): 775. https://doi.org/10.1186/s12884-022-05101-3.

Wong, Carlos K. H., Kristy T. K. Lau, Matthew S. H. Chung, Ivan C. H. Au, Ka Wang Cheung, Eric H. Y. Lau, Yasmin Daoud, Benjamin J. Cowling, and Gabriel M. Leung. 2024. “Nirmatrelvir/Ritonavir Use in Pregnant Women with SARS-CoV-2 Omicron Infection: A Target Trial Emulation.” Nature Medicine 30 (1): 112–16. https://doi.org/10.1038/s41591-023-02674-0.

Young, Jessica G., Lauren E. Cain, James M. Robins, Eilis J. O’Reilly, and Miguel A. Hernán. 2011. “Comparative Effectiveness of Dynamic Treatment Regimes: An Application of the Parametric g-Formula.” Statistics in Biosciences 3 (1): 119–43. https://doi.org/10.1007/s12561-011-9040-7.

Zidan, Mahmoud, Nhung T. H. Trinh, Anteneh Desalegn, Louisa H. Smith, Marleen M. H. J. Van Gelder, Hedvig Nordeng, and Angela Lupattelli. 2025. “BNT162b2 mRNA COVID-19 Vaccine Effectiveness in Pregnancy: Emulating Trial NCT04754594 Using Observational Data from Norwegian Health Registries.” Vaccine 68 (December): 127908. https://doi.org/10.1016/j.vaccine.2025.127908.